Uber v Taxis
Contents
Use the interactive simulation see for yourself.
Uber
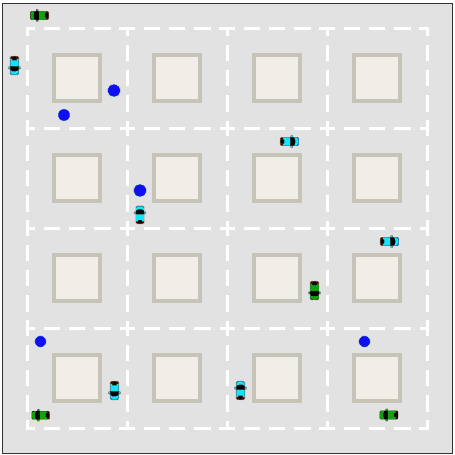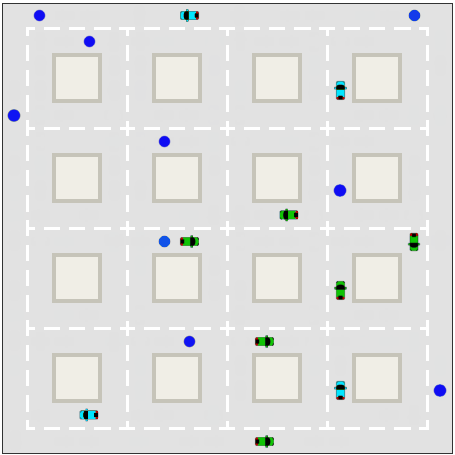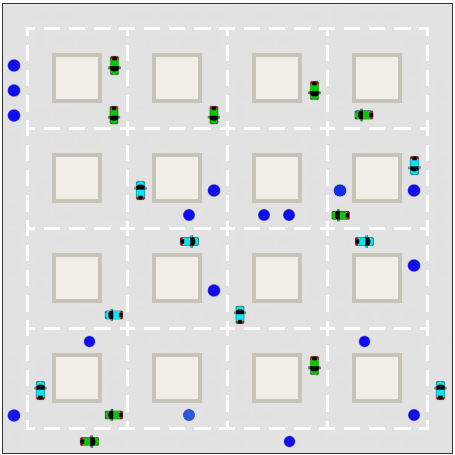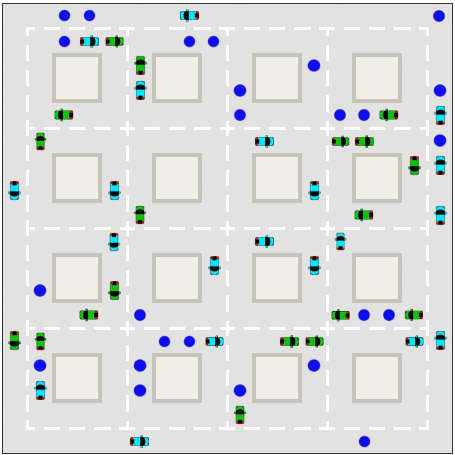
Taxi
"Prices formed a worldwide web of communication long before there was an Internet."
- Thomas Sowell, Basic Economics
1. Introduction
Uber, the ride-sharing company that connects freelance drivers with passengers via a smartphone app, gained a market valuation of over $41 billion in 2015. According to the company, its surge pricing scheme, whereby it raises prices during high demand to encourage more drivers to get on the road, is absolutely essential for it to "provide a reliable ride at all times"; something that taxis, with their fixed prices, cannot do. But the company's own customers apparently loath the inconsistent prices.1 Uber's real advantage, the customers might argue, is its fantastically user-friendly technology through which passengers can request a car, wherever they are, and watch on their phones as it drives to pick them up. Why does Uber muck it all up with an arcane pricing algorithm?
So what's more important to Uber's success, its surge pricing or its slick user interface? To find out we have developed an interactive simulation that removes Uber's technological advantage over taxis but keeps its surge pricing scheme. The simulation also includes a taxi-only world so you can compare Uber's dynamic pricing model to a more traditional fixed price taxi model. Here's how it works.
2. The Model
First and foremost it's important to understand that the simulation is just a model. As such, it is not meant to be a perfect replication of the real world with all its complexities; it is simply a representation based on reasonable assumptions that helps us study something not easily observable in the real world. In this case, we can't make Uber stop using surge pricing for the sake of science, so we'll have to build a model that lets us probe what the world might be like if they did.
In our simplified city, drivers (in either Uber cars or taxi cabs), randomly drive around square city blocks. When they come to an intersection, they shake a magic eight ball to decide whether to turn right, left, or go straight. Similarly, passengers will appear randomly throughout the city. When drivers and passengers end up in the same spot, the driver picks up the passenger and drives it (passengers are gender neutral in this simpler world) around for a random amount of time ranging from four to 100 minutes, whereupon the driver drops off the passenger and drives about until they pick up another passenger.
Since most cities tightly regulate both the prices charged by taxis and the number of cabs through mechanisms like New York's medallions, in our taxi world, both the price and the number of taxis are fixed.
As mentioned above, the Uber drivers do not receive requests from passengers and drive to pick them up. Just like taxis, they must drive around randomly to pick up passengers. The only difference between the taxi world and the Uber world is that Uber drivers respond to a price incentive that Uber can increase or decrease to get more or less drivers on the road. Uber implements its price incentive by multiplying its base rate by a "surge" multiplier. A 1X multiplier is the base rate, while 1.5X is one a half times the base rate.
While Uber's specific algorithm to calculate the surge multiplier is obviously proprietary, we have developed a reasonable approximation for our simulation. Basically, when the total time spent waiting by all passengers currently requesting a ride increases, the surge multiplier increases. When the total time decreases, the surge multiplier decreases.
Surge pricing relies on the assumption that when prices rise, more drivers get on the road. For example, the Uber driver Milton is sitting at home happily studying for his economics final. When the surge multiplier rises above say, 1.3X, Milton decides it's worth getting on the road to make some money. After he gives one ride to a passenger, the surge drops to 1.2X, but since Milton is already on the road he figures he'll drive around for a little bit longer. He picks up a few more passengers; but, after a while, demand has dropped enough that he isn't able to find a passenger for 10 minutes. So, he turns off his Uber driver app and returns to his economics studies.
Milton is just one of 100 Uber drivers in our simulation. To model how all 100 drivers might respond to the surge multiplier we use the distribution function shown below. It indicates how many drivers will be on the road for a given surge multiplier.
Uber Driver Incentive Curve
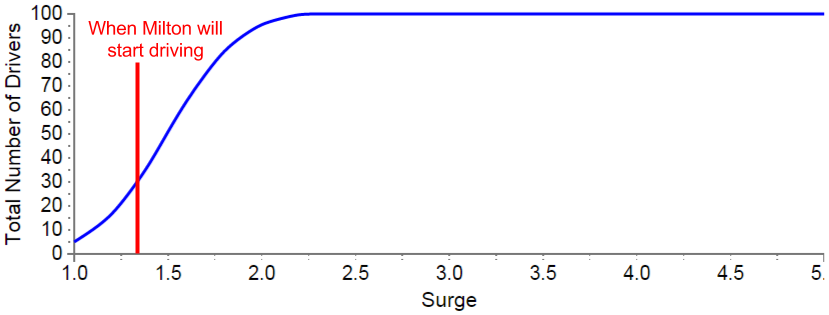
The above is a normal distribution function with a default mean surge of 1.5X and a standard deviation of 0.3X. According to this distribution, when the surge multiplier is 1X (i.e. the base rate), there will be five drivers on the road. When it rises to 1.1X, 5 new drivers will randomly appear somewhere on the road and begin driving. At 1.5X, 50 total drivers will be on the road, and at 2.2X, all 100 will be. When the surge drops back to 1X, all but the original five drivers will disappear from the road after they have not picked up a passenger in 10 minutes.
Real passengers can decide that the price of an Uber is too high or that it's not worth waiting for a cab. But for the sake of simplicity in our model, we're going to assume all passengers wait for a ride for as long as it takes and are willing to pay any price for that ride when it comes (although they may complain about it on Twitter later).
Outside of their own profit, both Uber and taxis have to balance at least three demands: the wait time of the passengers, the price of the ride and the drivers' income. It's important to realize that these three demands often conflict with each other, so Uber and taxis must balance trade-offs as best they can. The simulation keeps statistics on these three demands for both the Uber and taxi worlds so we can compare the results.
3. Constant Low Demand
Now that we have a simple simulation backed by reasonable assumptions, we can test how critical surge pricing is to Uber's success. Let's begin with a baseline case where demand is absolutely constant. From 12 PM to midnight there are always exactly five passengers requesting rides. Since this is the baseline case we'll keep the default settings as follows:
Constant Demand Settings
| Number of Taxis | 10 |
| Taxi Price per Minute | $0.25 |
| Uber 1x Surge Price per Minute |
$0.10 |
| Uber Max Surge | 1000 |
Here are the results for the constant demand case.2
Uber v Taxis - Constant, Low Demand
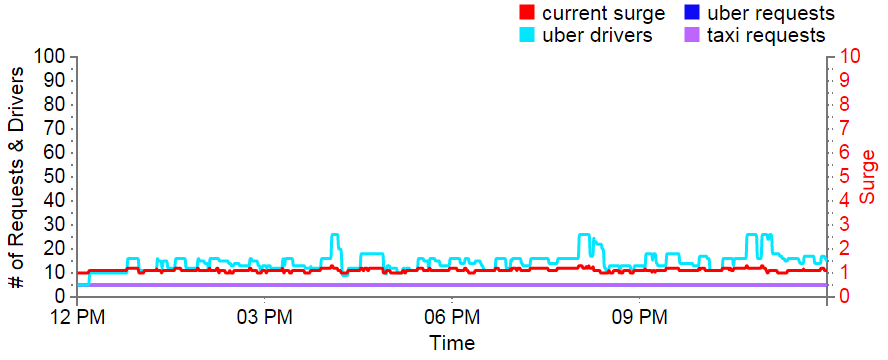
| Average wait time | Longest Wait time | Average price per minute | Average driver salary per hour | Total Rides Completed | |
|---|---|---|---|---|---|
| Taxi | 00:25:00 | 02:16:00 | $0.25 | $7.12 | 133 |
| Uber | 00:19:30 | 01:42:30 | $0.11 | $2.93 | 174 |
Even though Uber averages approximately 10 cars on the road, the same as the fixed number of taxis, it's average wait time is significantly, though not hugely, lower. Because drivers and passengers must randomly end up in the same spot, a passenger can end up waiting for a long time, even if demand is constant. When that happens, Uber can increase its supply of cars to reach the waiting passenger faster. This is most evident in Uber's much smaller Longest Wait Time. In this constant low demand case, Uber's surge pricing acts as a sort of wait time variance dampener, ensuring that any given passengers isn't going to wait an absurdly long time. Of course, the decrease in wait time variance comes with an increase in price variance.
Unsurprisingly, the Uber rides are significantly cheaper because Uber's base rate (1X) is lower than the taxi's fixed rate. Taxis have to maintain a high fixed rate because the drivers must be compensated for times of low demand (like this one) when they spend a great deal of time driving around without any passengers. One way to think about how taxis solve the pricing problem is by making the low demand passengers subsidize the high demand passengers.
While the passengers of the Uber world get a great deal, the drivers get hosed. Their average salary is only $2.93 per hour. Most drivers will not remain drivers for long with this measly income, so Uber's model, a low base rate with surge incentives, doesn't really work in this constant low demand case. The taxi's fixed price model is the only one that's sustainable. However, the real world does not have a constant demand.
4. Changing Demand
So what happens when the demand changes? In particular, we'll be interested in what happens during a large spike in demand.
The "Auto-change Demand" option in the simulation creates several spike throughout the day. Here are the results.3
Uber v Taxis - Changing Demand
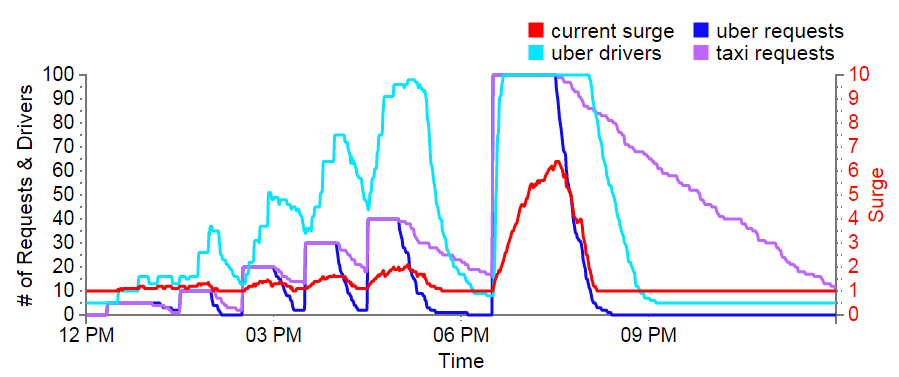
| Average wait time | Longest Wait time | Average price per minute | Average driver salary per hour | Total Rides Completed | |
|---|---|---|---|---|---|
| Taxi | 01:50:30 | 06:15:00 | $0.25 | $11.01 | 208 |
| Uber | 00:16:30 | 01:37:00 | $0.27 | $11.09 | 737 |
Let's consider the taxis world first.
Taxis - Changing Demand
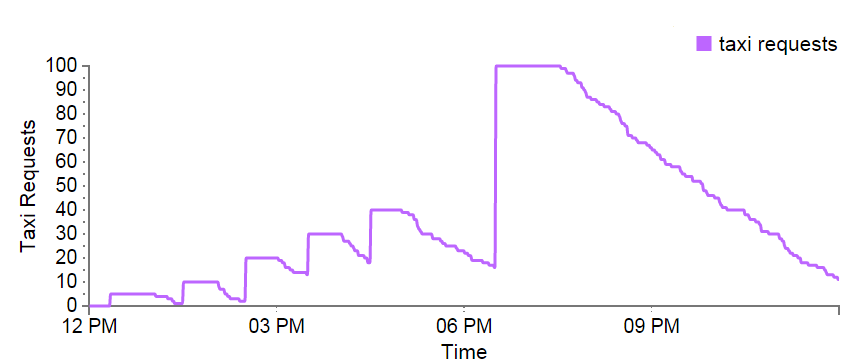
At the very beginning, things are much like the constant demand case. But as demand starts to step it's way up between 1:30 and 4:30, it becomes harder and harder for the 10 taxis to keep up with the requests. At the beginning of the 6:30 spike in demand they haven't even serviced all the requests from the 4:30 rise. Finally during the 6:30 spike, the kind that would occur after a huge concert in downtown Manhattan, the taxis simply cannot cope with the demand. Even though the number of new requests drops to zero after the spike, the taxis still take hours to pick up all the passengers. At midnight, four and a half hours after the spike ended, there are still 15 requests that haven't been fulfilled.
Simply put, in a world with highly variable demand, the fixed supply of taxis cannot fulfill all the ride requests.
But does Uber do any better? Simply put, yes.
Uber - Changing Demand
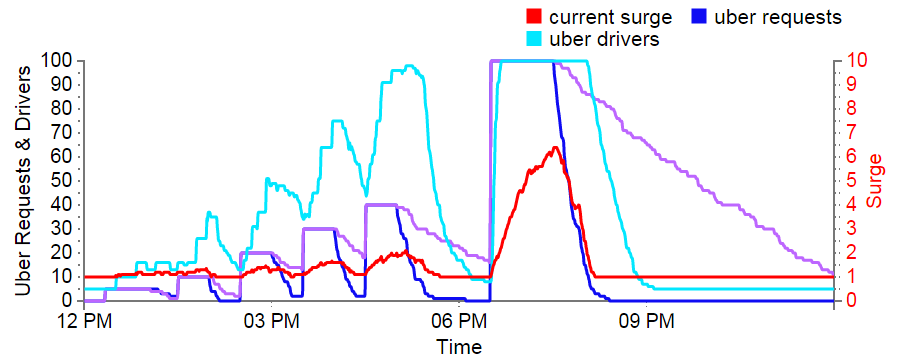
The smaller steps earlier in the day that quickly overwhelmed the taxis are easily handled by Uber. From noon to 6PM, even though the surge multiplier only fluctuates between 1X and 2X, the supply of drivers fluctuates between five and 95. Equally importantly, when the surge multiplier drops, these drivers get off the road and find something better to do with their time. That allows Uber to keep their base rate lower without torpedoing the driver's salary.
During the 6:30-7:30 spike Uber really shines. All passengers got a ride by 8:30. In under an hour, Uber handles what takes the taxis more than four and a half hours. Because Uber provides rides faster, it can provide rides to many more passengers; in this case 737 to the taxi's meager 208.
However, all this convenience comes at a cost. The surge multiplier peaked at 6.5X, which means passengers were paying $0.65 a minute during the spike, while the taxi passengers were paying only $0.25 per minute. But this price difference is really an illusion. The only passengers who paid $0.25 per minute were those lucky enough to get a ride. The others were left out in the cold for hours with no way to get home. Furthermore, in the real world, the Uber passengers who don't want to pay the surge price can wait an hour for it to come down to $0.10 and still get home hours before their taxi world compatriots.
This is the real power of dynamic pricing. The yuppie parents who need to get home ASAP to relieve the babysitter can pay the extra money during the surge. Meanwhile, the poor college kids can wait it out at a bar and, even with the added beer cost, still get home cheaper and faster than they can in a fixed-price world.
It's also worth asking how our model compares with reality at this point. While we don't expect the surge multiplier, price per minute, etc to match the real world, we do expect the trends of our surge multiplier and driver supply to be consistent with Uber's real world trends. Fortunately, a paper by the Chicago Booth School of Business tested the effects of the surge multiplier using Uber's data. Here is a graph from their paper.
Uber Driver Supply and Ride Requests After a Sold Out Concert
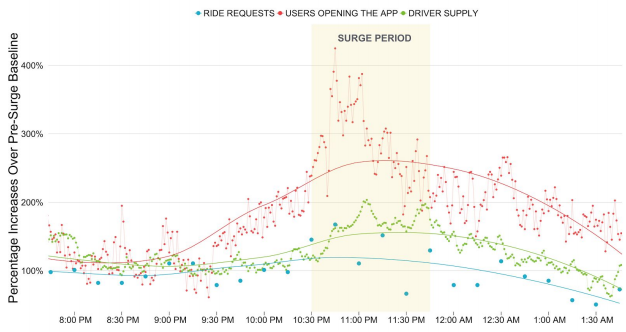
Just like our simulation, during a surge period the supply of Uber drivers rises as the number of ride requests increases, levels off as the demand is met, and returns back to normal as the demand returns to normal. Our simulation looks like it's at least a good approximation of reality.
What about the Uber drivers? Even though the average price per minute in the Uber world is only $0.02 higher than the taxi world, the Uber drivers' average hourly wage is $.07 higher than the taxi drivers. Now it's important to realize that this is an average. The drivers who only hit the road for the 6:30 spike made a lot more per hour than the original five drivers who were pounding the pavement the entire day.
Is this fair? Again the power of dynamic pricing is made manifest. The five drivers who have the time and need the money the most, maybe they're between jobs at the moment, are willing (but maybe not happy) to drive throughout the day. Those who need to study for their Economics finals are only willing to drive during the 6:30 spike. In a heavily regulated, fixed price world, the five potential Uber drivers who need the money the most will make exactly zero dollars sitting at home, while the potential spike-drivers will use their study breaks to watch Gilmore Girls instead of putting their economics knowledge into practice. All while the yuppies and the college kids are left out in the below freezing weather, fighting over the ten available taxis.
5. Emergencies
There is one final case worthy of our attention. Uber has provoked absolute outrage and accusations of price-gouging several times because its algorithm steeply increased prices during emergencies like Hurricane Sandy in New York and the hostage situation in Sydney. It's all well and good that Uber provides yuppie parents and drunk college kids a way home on a Saturday night, but even the most ardent Uber supporters wouldn't condone the use of surge pricing during an emergency, right?
Let's see if we can use our simulation to model the potential trade offs of surge pricing during an emergency like Hurricane Sandy. In an emergency, demand for transportation is high because public transit is either limited or out completely and taxis are not driving either. Because of the horrible conditions, naturally Uber drivers don't want to be on the road either. To get drivers on the road, and here's the rub, Uber claims it must raise its prices significantly.
To model the decrease in the supply of Uber drivers, we will adjust the Uber Driver Incentive Curve such that they will require more money than usual to drive through the 80 MPH winds and flooding waters. Here's what our new incentive curve looks like with a mean of 5X and a standard deviation of 0.8X.
Uber Driver Incentive Curve - Emergency
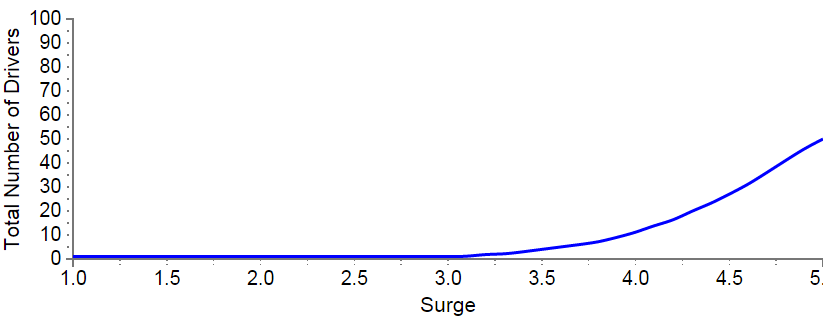
Notice that hardly anyone is going to drive for less than a 3X multiplier and that even with a 5X multiplier only half the usual 100 drivers will be out. I've also reduced the number of taxis to five to reflect the decrease in their supply of drivers.
During an emergency like Hurricane Sandy, demand probably doesn't really spike like it does after a concert or on a Saturday night. Rather, it's consistently high, without any huge spikes. As such, our demand will fluctuate between 40 and 60 - until about 10PM, when it will drop off completely.
Okay, now that we have a reduced supply of drivers and a high, fluctuating demand let's see the results.
Uber v Taxis - Emergency
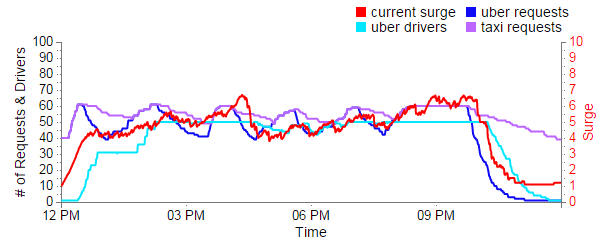
| Average wait time | Longest Wait time | Average price per minute | Average driver salaryper hour | Total Rides Completed | |
|---|---|---|---|---|---|
| Taxi | 03:19:00 | 11:54:00 | $0.25 | $13.06 | 111 |
| Uber | 00:33:00 | 05:18:00 | $0.51 | $25.99 | 957 |
From the graph you can see the surge multiplier is drastically higher than normal. Once the simulation gets going it ranges between 4X and 7X, so the passengers are paying a heck of a lot more money than usual. This is also reflected in the Average Price per Minute which is more than double the taxi's price. So far it looks like Uber really is price gouging people when they need a ride the most.
However, the demand for rides is much higher than normal and the supply of rides, both Ubers and taxis, is much lower than normal so rides are much more scarce.
In the fixed price world of taxis, there simply aren't enough rides for everyone who needs one. Thus, the taxi world can only use random chance, whoever happens to catch a cab first, to allocate the scarce rides to passengers. The passengers lucky enough to flag down a ride will get one, while the rest will be left out in the rain.
But the dynamically priced world of Uber has another lever to pull. By increasing its prices, Uber can incentivize more drivers to brave the weather, thus providing more rides to passengers that the taxi world leaves out in the rain.
Uber will, however, be charging higher prices, and some potential passengers will not be able to afford the ride. So it's reasonable to ask if this is fair. From the driver's perspective it certainly is. They are braving the weather when everyone wants to be safe at home. They're taking on risk and rightly deserved to be compensated for it.
But what about the passengers who can't afford Uber's higher prices? In the fixed price world most of them still won't get a ride, but some will be lucky enough to snag one. Is randomly allocating scarce rides fair? I don't know. But either way, fairness isn't the only thing that matters.
According to the simulation, Uber is able to service 957 passengers to the taxi's 111. That's 846 more people who can save their possessions from the flood, or who can bring food home to their children, or who can take care of an ailing parent. And that is certainly worth something.
6. Conclusion
The final example and its real life analogies of Hurricane Sandy and the Australian Hostage Situation show that questions about Uber's surge pricing are not just trivial matters of providing a convenient ride home to concert attendees. It also conjures deeper moral questions about what we value in society.
Surge pricing seems unfair on the surface, but ultimately it provides more rides for more people by relying on market pricing. In The Better Angels of Our Nature, Steven Pinker says the market pricing model of morality "requires the nonintuitive tools of symbolic mathematics" that "allows one to reason in terms of proportionality". In other words, surge pricing feels so wrong because our brains did not evolve to understand the complex relationships between supply, demand, and price. But with the help of mathematics, economics, and computer simulations we can better understand the constant trade-offs involved in the allocation of scarce resources like transportation.
As stated, this simulation is not a precise recreation of reality. It is a simulation. But those who want to pretend that we live in a world without scarcity or where people don't respond to incentives are not recreating reality either. They are imagining a fiction. So long as we are stuck with each other in this world, dynamic pricing will continue to be critical to Uber's success... And ours.
1. All of the articles we could find rely on Twitter outbursts from Uber users (particularly Jerry Seinfeld's wife) for evidence. Perhaps all the controversy indicates is that people don't like to pay more money.^
2. Note that if you run this or any other case yourself you will receive slightly different results because in the simulation, as in the real world, there is a great deal of randomness.^
3. You can easily recreate the results yourself. Try it with different inputs settings and see how you can balance Wait Time, Ride Cost, and Driver Salary for both the Taxi and Uber worlds.^
 Socratic Owl
Socratic Owl